Intro/FAQ ⎜ Episode 1 ⎜ Episode 2 ⎜ Episode 3 ⎜ Episode 4 ⎜ Episode 5 ⎜ Episode 6 ⎜ Episode 7 ⎜ Episode 8 ⎜ Episode 9 ⎜ Episode 10 ⎜ Episode 11 ⎜ Episode 12 ⎜ Episode 13 ⎜ Episode 14 ⎜ Episode 15 ⎜ Episode 16 ⎜ Episode 17 ⎜ Episode 18 ⎜ Episode 19 ⎜ Episode 20 ⎜ Episode 21 ⎜ Episode 22 ⎜ Episode 23
[Editor’s Note: This is the nineteenth in a series of 23 essays summarizing and evaluating Book of Mormon-related evidence from a Bayesian statistical perspective. See the FAQ at the end of the introductory episode for details on methodology.]
The TLDR

It seems unlikely that the similarities we can observe between Egyptian/Semitic and Uto-Aztecan languages could have arisen by chance.
Few Book of Mormon-related discoveries have had as much impact or have generated as much controversy as Brian Stubbs’ proposal connecting Egyptian and Semitic with the Uto-Aztecan languages of northern Mexico and the southwest U.S. Highly credentialed experts have weighed in both for and against, but little has been done to definitively settle the question. Using a sample of 200 of Stubbs’ 1500+ correspondences, I do my best to estimate the likelihood of seeing those connections by chance. That likelihood appears to be quite low indeed. My analysis suggests that chance could produce as many as 235 correspondences out of 2700 identified proto-Uto-Aztecan words, corresponding to a 3% chance per word for each near-eastern language Stubbs attempts to compare them against. When limiting Stubbs’ proposal to only those correspondences that implicate proto-Uto-Aztecan, and whose meanings match exactly or near-exactly, and assuming that Stubbs himself has an error rate of 20%, I estimate that there’s a core set of 422 correspondences that meet those criteria. Though 422 might not seem like that much more than 235, the probability that Stubbs could have reached that many by chance is p = 6.99 x 10-15. As much as many might believe or wish otherwise, Stubbs’ work can’t be easily dismissed.
Evidence Score = 14 (increases the probability of an authentic Book of Mormon by 14 orders of magnitude).
The Narrative
When last we left you, our ardent skeptic, you had set aside your annoyance at the fallibility of so-called “prophets,” and you press on with the war and bloodshed that stains the book’s pages. You become weary enough of it that you take a moment and hold the book by its spine, keeping your place with a finger. Over two-thirds of the way through and yet you have no clue where this story is leading. Just conflict interspersed with the occasional sermon, like bittersweet raisins spread in a sour pie.
But you can’t sit long without sating your curiosity, and you again return to reading. To your near shock, within a chapter the war is over, and the narrative moves away from it almost immediately. In the wake of war there’s peace, and peace, apparently, begets boredom. An enigmatic character named Hagoth directs his boredom to building boats, and to convincing others to sail away from their homeland in order to settle the lands to the north.
You muse that Hagoth must have been an exceptionally talented con man to have convinced anyone to engage in that kind of insanity. Yet the travelers apparently returned, their voyage successful, with Hagoth sending additional rounds of settlers northward.
That sets your mind turning. Obviously these Nephites and Lamanites, if they existed, should have left their mark on the lands and culture surrounding them. But you wondered what sort of mark these expeditions might have had on whatever “northward” lands they sailed off to. You think about other voyages of settlement and conquest, and the effects that those had—the Spaniards who settled the Philippines, their language altering forever the Tagalog of the natives, or English being suffused with the Scandinavian of Viking hordes. Perhaps the key to discovering the truth of this book was in the languages of that northern land.
These thoughts echo within you, and not just metaphorically. You can actually hear the word “land” reverberate between your ears. But each time you hear it the word seems to change, as if it was being subtly shaped by the contours of your mind. Eventually the sound seems to converge into a different word entirely:
“daama”
Based on your past studies, you recognize it as the Hebrew word for “land.” But it doesn’t stay in that form for long. After a moment, it takes the form of yet another word:
“tima”
You don’t know how you know, but somehow you also recognize this word. It also meant “land,” but it wasn’t Hebrew. You see in your mind’s eye a land far to the west of your own New England, toward the western shores of northern Mexico. The word belonged to these people—not to those who lived there in the present, but to those who inhabited it anciently.
No. You think. This can’t be possible. But now the word “no” begins to echo, slowly transforming into another word.
“bi”
For a moment you don’t think you know the word, but then suddenly you do. It also means “no,” but the word was far more ancient than English, and had been spoken by the same people who had erected the pyramids of Egypt. But that word also changes into another, though the change is slight indeed.
“pi”
The way the “p” sound formed was only barely distinguishable from the previous “b.” You knew that this word, too, belonged to the indigenous people inhabiting the lands of northern Mexico.
As the echoes continue you sigh inwardly. This isn’t the first time the book had driven you mad. What have I done to be smitten with this malady? you think. But now the word “smitten” begins its echoic journey around your skull, the "s" and the "n" fading away, and the "I" and "tt" changing their shape:
“mukke”
This word is also Hebrew, yet strangely you know that it’s of a different sort, a Hebrew that had itself been influenced by the Jews’ Phoenician neighbors. As the echo continued it too stayed almost the same, but you could make out a minor difference:
“mukki”
In the moments that follow you seem to hear not just those words, but hundreds upon hundreds of others. Each word—whether Hebrew or Egyptian—would turn into another spoken by the ancient inhabitants of that area of the American continent. Sometimes the change would be subtle, other times it would be more significant, but always you could hear the ways that one changed into the other. As the cacophony of words finally begin to fade away, you mind calls back with unnatural clarity to words you had read at the beginning of the book, at what had been the second verse in the very first chapter:
Yea, I make a record in the language of my father, which consists of the learning of the Jews and the language of the Egyptians.
As the verse finishes you throw the book down at the table so hard that you fear for the integrity of the table. With an urgency that approaches terror you push yourself up from your chair and storm out your door into the afternoon sun. You try hard, between heavy breaths, to regain your composure, but as your heartbeat slows and your lungs calm, a thought remains lodged in the front of your brain. If there really is a language in the Americas that appears to have been influenced so strongly by Hebrew and Egyptian, it seems unlikely that such similarities could have arisen by chance.
The Introduction
For the past couple hundred years linguists have been consistently dogged by a claim that, on its face, seems patently ridiculous—the idea that the languages of Indigenous peoples have been influenced by Hebrew, whether by descent or by contact. Though this claim has not been unique to Latter-Day Saints (it was believed by many Christians in early America that the New World had been home to the lost ten tribes), such evidence, if it existed, would have obvious implications for the authenticity of the Book of Mormon. Yet, as the decades passed, each claim of a connection to the Hebrew language was proven to be spurious, a fact that has left scholars increasingly and justifiably jaded with each new claim.
But in recent years a claim has arisen that is very difficult to dismiss out of hand. Brian Stubbs, a respected linguist and noted expert in the Uto-Aztecan language family, has spent the better part of four decades patiently collecting an apparent mountain of linguistic evidence showing just that kind of Hebrew connection. That evidence seems to indicate that, several thousand years ago, there was extensive contact between the languages of that family and a mix of Semitic and Egyptian—a mix that just happens to align with what the Book of Mormon would predict for its peoples. This evidence uses the same general methods that linguists would use to establish relationships between different languages, and the volume of that evidence does indeed appear to be impressive, with over 1,500 detailed word correspondences connecting the Old and New World languages.
Unsurprisingly, Stubbs’ claims have not gone unchallenged. A number of linguists have been intrigued by his claims and satisfied with his methods, but others have not. In each case the critics have maintained that it would be possible to see that many correspondences by chance, particularly given the number of languages that Stubbs has drawn from to create his language sets. Unfortunately, the math underlying that assertion has, so far, been sub-par. And that, hopefully, is where Bayes can come in. Bayesian analysis is just the sort of tool that could serve to resolve this dispute, though the linguistic nuances involved make this by far the most challenging problem we’ve tackled so far.
The Analysis
The Evidence
There’s not much point trying to summarize the evidence, since it’s already been done so ably. If you don’t want to bash your head against Stubbs’ own extensive 400 page analysis (from which I’ve pulled the data I’m using here), you could take a look at his more accessible book, or read/watch his 2016 FairMormon Conference talk. You could also sample Jeff Lindsay’s summary in Interpreter, or the positive reviews from two separate BYU linguists.
But if you wanted an elevator pitch, here it is: there are many, many, many words that appear, to an extent, shared between Egyptian and Semitic on one side and the 61 languages that make up the Uto-Aztecan language family on the other, whose speakers were centered in northern Mexico and the American southwest, including the Pacific coasts of those areas. It is worth noting that these areas would be conspicuously accessible to seafaring migrants moving northward from the Pacific side of the Isthmus of Tehuantepec. Here’s a map, in case you’re curious:
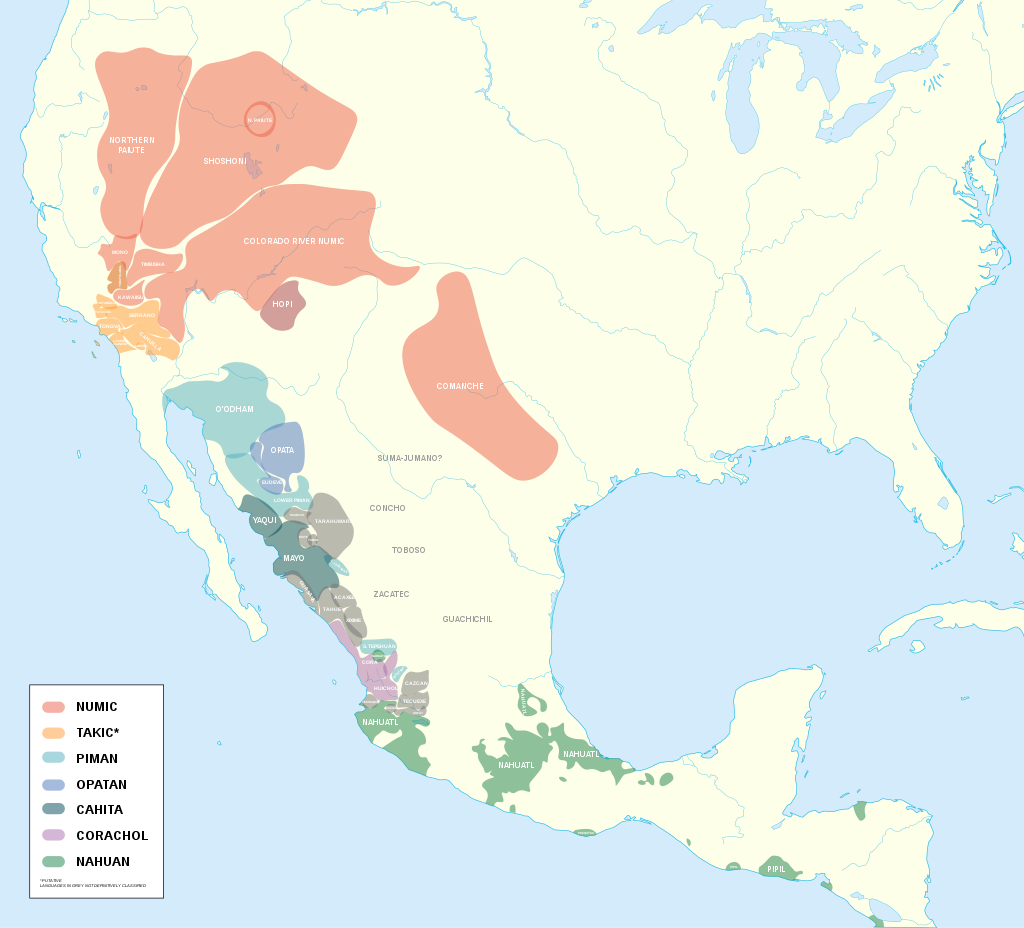
Now, as you might expect, not all of those correspondences are perfect matches. But the differences aren’t just random—they point to consistent changes in sound that make sense given how languages commonly shift, such as changes from b sounds to p sounds, or l sounds to r sounds. And, according to Stubbs, the connections with Egyptian and Semitic help solve a number of mysteries that scholars of Uto-Aztecan had been trying to solve for years.
Over the last couple years there have been two key critiques of Stubbs’ work. The first is a paper from Chris Rogers, a linguist at BYU publishing in the Journal of Mormon Studies. His key argument (and the only one with real force) is that because Stubbs made use of multiple related languages in his search for correspondences (i.e., multiple Semitic languages, and, of course, the many different languages of Uto-Aztecan), he was fishing in too large of a pool—if you search enough words in enough languages, you will unavoidably find words with similar meaning that sound the same. Rogers even included a rather ill-advised table attempting to demonstrate this idea, one that makes some terrible assumptions, including that each of the languages are independent of each other (they, of course, aren’t independent, since they’re in the same language family). But despite Rogers’ error, he does have a point—searching in more languages would indeed lead to more false correspondences.
The second critique came from Magnes Hansen, a fellow Uto-Aztecan expert specializing in the Nahuatl language. Hansen took a look at 14 correspondences relating to his specific language of expertise, and came away mostly unimpressed, arguing that the correspondences aren’t as good or as proper as Stubbs seems to claim. Stubbs has since responded to both Rogers and Hansen in-depth in this article.
In this analysis, I can’t say much about whether those correspondences are proper—whether they follow the rules of linguistic analysis. All I’ll be able to do here is try to determine whether they’re expected—whether we could get a similar result just by examining any comparable set of unrelated languages.
But first, the hypotheses.
The Hypotheses
Linguistic correspondences with Uto-Aztecan are due to contact with Book of Mormon peoples—With this theory, the linguistic correspondences observed by Stubbs can be most readily explained by contact between Uto-Aztecan speakers and the people’s described in the Book of Mormon, peoples who would have been speaking just such a hybrid of Egyptian and Semitic, and who would have been traveling the the coasts of Mexico and California at around the right time-depth to have influenced the appropriately ancient form of Uto-Aztecan.
Linguistic correspondences with Uto-Aztecan are due to chance—This theory posits that the correspondences found by Stubbs could appear by chance—that by looking at enough words and enough languages, eventually Stubbs was bound to find words in Egyptian and Semitic that appeared similar to Uto-Aztecan languages just on the basis of random variation, and that this can happen with any set of languages.
Prior Probabilities
PH—Prior Probability of Linguistic Contact—Given the various types of evidence we’ve considered up to this point, we’re very much obliged to give Stubbs’ proposal the benefit of the doubt, with a prior probability of p = 1 – 2.07 x 10-19. As always, here’s a review of where we’ve been so far:
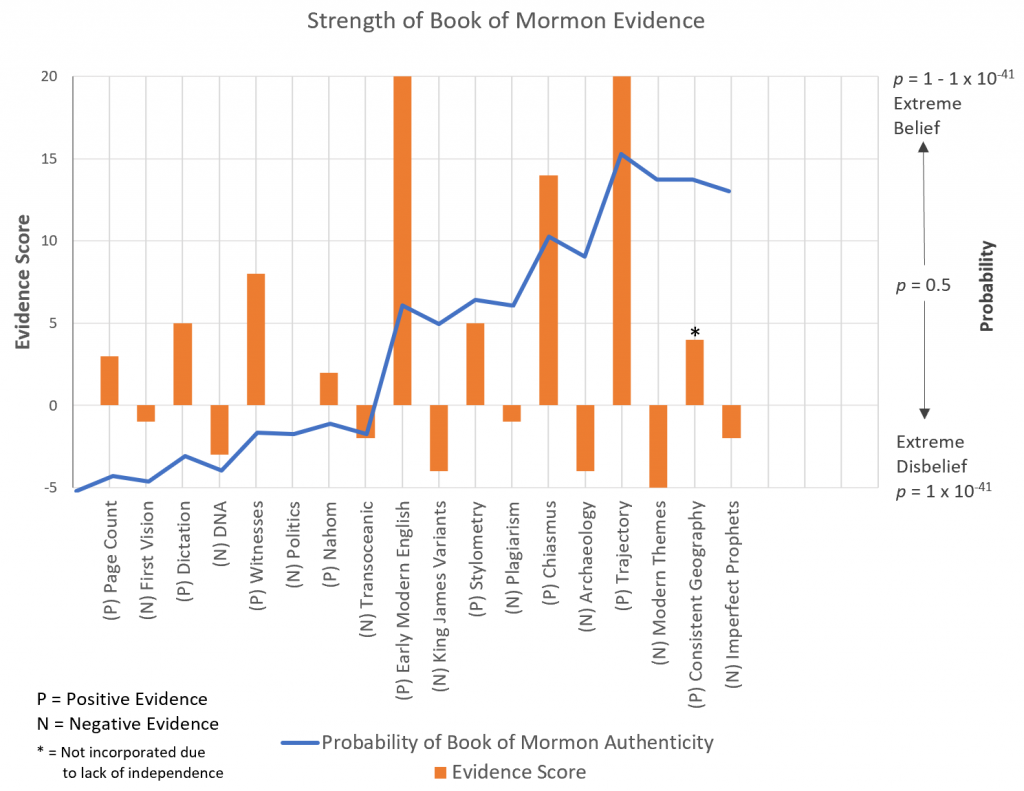
PA—Prior Probability of Chance-Based Correspondence—Despite the slight boost provided by the prophetic errors outlined in the previous episode, our prior for the critical hypothesis is an anemic 2.07 x 10-19.
Consequent Probabilities
CH—Consequent Probability of Linguistic Contact—Our first job is to figure out how likely we would be to see Stubbs’ correspondences if his theory was correct, which, thank heaven, is a mercifully simple task. Out of all the criticisms leveled at Stubbs’ work, never have any of them said “no, this can’t be contact, because contact doesn’t look like this.” Part of that, I suspect, is that contact could essentially look like anything. There’s no verse in the Book of Mormon that says “lo, and Hagoth’s settlers landed, and had just enough contact to product 300 linguistic correspondences and no more.” There could’ve been a lot of contact or there could’ve been a little. Based on what Stubbs explains, that contact appears to be relatively extensive, with correspondences covering a substantial proportion of the language. But I see no basis in the evidence itself to rule out the type of contact we’re considering. I’ll be assigning a consequent probability of p = 1.
CA—Consequent Probability of Modern Authorship—Our much more difficult task will be evaluating the idea that such correspondences could arise from chance. As noted above, the initial effort from Rogers is of little use to us. He does reference the idea that we might expect between 1% and 3% of correspondences between any two related languages to have arisen by chance (for which he cites Stubbs!), but that doesn’t tell us much about what we’d expect from Stubbs’ correspondences, or from these particular languages. That chance could well be lower (or higher) for the correspondences at which Stubbs was actually looking. If we’re serious about getting this right, that means taking a hard look at the correspondences that Stubbs actually reports.
This thought didn’t exactly fill me with glee, given the breadth and density of Stubbs’ full report. So, I did what any hot-blooded experimental social psychologist would do: I took a random sample.
In particular, I randomly selected 200 of Stubbs’ 1,528 correspondences (I used the RANDBETWEEN function in Excel in 200 cells—if a number was picked twice I altered it to be the previous number), keeping track of a variety of information for each. For both the Old World word in the correspondence (which I termed the “source") and the Uto-Aztecan word (which I termed the “target”), I entered the specific language the word came from, the meaning of the word, the number of consonant-level sounds, and what those sounds were, associating each sound in the source word with the corresponding sounds in the target word (which would let me keep track of whether or not each sound matched). Since the Hebrew and Egyptian words often lacked vowels, vowel sounds were generally excluded. You can take a look at the appendix for the full table, if you have the requisite courage.
WARNING: We’re about to get very deep in the weeds here—if that sort of thing makes you squeamish (or bored) you may want to look away now. I’ll let you know when it’s safe to pay attention again.
Based on that table, I could estimate a few things about Stubbs’ correspondences, things that should generalize pretty well to the full set. The first was the sounds themselves and how they correspond. One thing that’s hard to get a sense of from just reading through Stubbs’ sets is just how well the words match. Some of them match very well, with a substantial number of sounds lining up well with little variation. Others share only a sound or two, with some of the target words adding sounds not found in the source or missing some of the source sounds. From the table below, though, we can see that about half (54%) of the sounds in the source are a match for the ones in the target, with another 14% having similar sounds that Stubbs posits could have shifted systematically over time. However, a number of others were either not matching or had been dropped (16% each). You can take a look at that in the table below:
| Source Sound | Matching | Similar | Not Matching | Dropped | Total | % of Source Sounds | |
|---|---|---|---|---|---|---|---|
| ‘ | ‘ (6) | w (8) | 14 | 8 | 36 | 6.4% | |
| ? | w (9) | 6 | 5 | 20 | 3.5% | ||
| b | b (5) | p (21) | kw v(5) | 3 | 6 | 40 | 7.1% |
| d | d or t (17) | 7 | 2 | 26 | 4.6% | ||
| f | 2 | 0 | 2 | 0.4% | |||
| g | g (2) | ng (4) | k (9) | 0 | 2 | 17 | 3.0% |
| h | h (14) | ‘ (5) | 3 | 4 | 27 | 4.8% | |
| i | i (8) | y (2) | e (1) | 1 | 5 | 17 | 3.0% |
| k | k (8) | c (2) | 3 | 3 | 16 | 2.8% | |
| l | l (12) | r (3) | 3 | 10 | 28 | 5.0% | |
| m | m (33) | 0 | 1 | 34 | 6.0% | ||
| n | n (23) | 3 | 5 | 31 | 5.5% | ||
| p | p (24) | b (1) | 4 | 0 | 29 | 5.1% | |
| q | q or k (25) | 5 | 4 | 34 | 6.0% | ||
| r | r (15) | y (6) | t (7) | 24 | 14 | 52 | 9.2% |
| s | s (40) | c (13) | 0 | 4 | 57 | 10.1% | |
| t | t (40) | 4 | 9 | 53 | 9.4% | ||
| th | 1 | 0 | 1 | 0.2% | |||
| v | v (1) | 0 | 0 | 1 | 0.2% | ||
| w | w (14) | v (2) | u (2) | 3 | 4 | 25 | 4.4% |
| x | k (6) | 2 | 1 | 9 | 1.6% | ||
| y | y (14) | i (3) | 2 | 3 | 22 | 3.9% | |
| z | c or s (3) | 0 | 0 | 3 | 0.5% | ||
| Total | 304 | 81 | 90 | 90 | 565 | ||
| % | 53.8% | 14.3% | 15.9% | 15.9% | |||
Another important piece is how the number of sounds themselves line up. The more sounds a word has, the less likely it will be for a certain proportion of those sounds to match. But the number of sounds aren’t going to be evenly distributed, and could be distributed differently for each language. The next number shows how often the correspondences featured words with a certain number of sounds. The rows represent the number of sounds in the source word, and columns represent the number of sounds in the target:
Number and Proportion of Sound Combinations
| Source | Target | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 4 (2.0%) | ||||
| 2 | 27 (13.5%) | 9 (4.5%) | 2 (1.0%) | ||
| 3 | 45 (22.5%) | 77 (38.5%) | 9 (4.5%) | ||
| 4 | 8 (4.0%) | 11 (5.5%) | 3 (1.5%) | ||
| 5 | 4 (2.0%) | 1 (0.5%) | |||
Using information from the above two tables, we can calculate a probability for each pairing of sounds in the source and the target—in other words, for each cell in the second table. This gets a bit complicated in practice, but the general principles are pretty simple—we want to calculate the likelihood that a certain number of target sounds will match the ones in the source, and that “certain number” is equal to half (we’ll say half instead of 54% for the sake of simplicity) of the number of target sounds.
I’ll give you a few examples, and I’ll start with a simple one: the case where there are 4 sounds in each of the source and target words. Based on my sample, there are, in effect, 19 different consonant-level sounds in Uto-Aztecan (there are fewer actual consonants, but I’m going by how they’re transcribed into English, as well as assuming that d and t as well as k and q represent the same underlying consonant. We need to figure out the probability that half of those sounds would match. We can show that for each sound, 1st, 2nd, 3rd, and 4th:
(1/19) (1/19) (18/19) (18/19)
In this case, the odds of getting a sound match would be 1 in 19, while the odds of not getting a sound match would be 18 in 19. By multiplying those probabilities together, we can calculate the probability that this specific combination of sound matches will occur, which, in this case, would be as follows:
p = (.053) * (.053) * (.947) * (.947) = .0025
But that’s not the only combination of matching sounds we could run into. We could also have the 1st and 3rd sound match, with the 2nd and 4th sounds not matching. Or we could have the 1st and the 4th sounds match, or the 2nd and 3rd, etc. All told, there are 6 different combinations. To account for that, we multiply the probability above by 6.
p = .0025 * 6 = .015 = 1.5%
So if the source and target each have four sounds, there’s about a 1.5% chance that two of those sounds will match.
As I said, that was the simple example. Things get a little more complicated for other combinations. For example, if we have 5 sounds in the target, and 4 in the source, we’d have to calculate that two and a half of those sounds match. You might justifiably ask how you can get a probability for half of a match. In short, you don’t—at least, not directly. What you do is take note of the probability that two sounds match (1.5%) and also calculate the probability that three of those four match:
(1/19) (1/19) (1/19) (18/19)
p = (.053) * (.053) * (.053) * (.947) = .00014
Since there are 4 possible combinations of matching sounds in this case (where the 1st, 2nd, 3rd, and 4th sounds don’t match, respectively), we multiply that value by 4 to get the total probability that 3 of the 4 sounds match.
p = .00014 * 4 = .00056 = .056%
So, the probability that 2 of the sounds will match is 1.5% and the probability that 3 of the sounds will match is quite a bit less, at .056%. It stands to reason that the probability of two and a half of those matching is somewhere between the two, and our best guess for that will be the average of those two values.
But it doesn’t make sense to just calculate a regular old mean and call it a day. The relationship between the probability and the number of sounds that match isn’t linear, with that value approaching zero the more sounds need to match. To demonstrate this, you can take a look at the figure below:
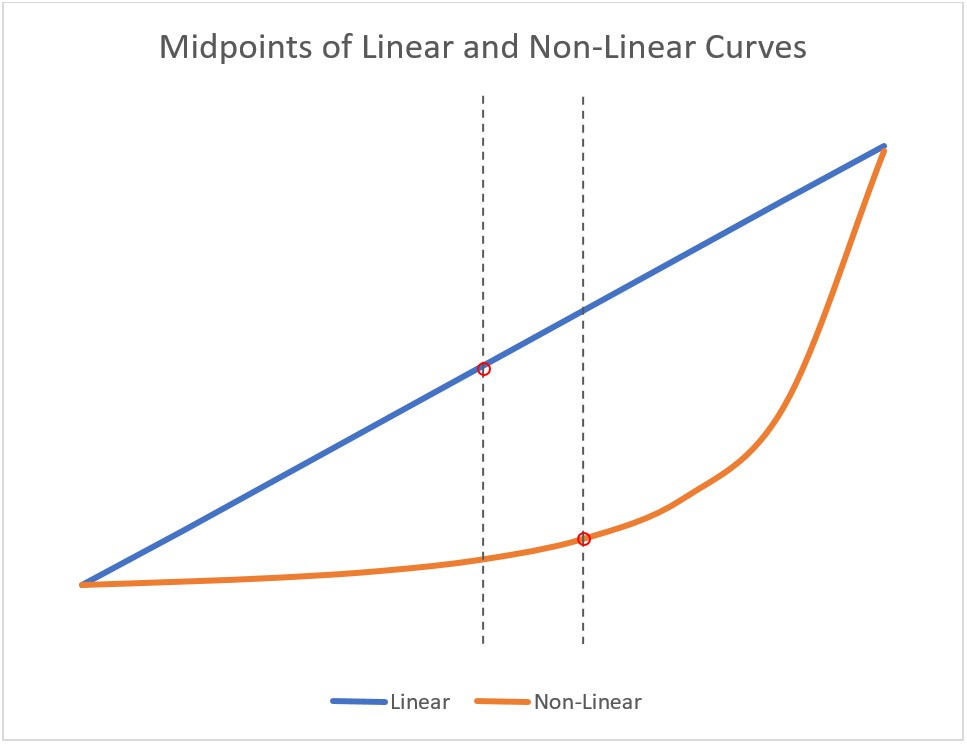
Taking the regular or “arithmetic” mean is like trying to find the middle of that straight line. But the probability doesn’t function like the straight line—it functions like the curve. And the middle of the curve is quite a bit lower than the middle of the straight line. So the more accurate “average” in this case isn’t going to be in the numeric middle, which would be .784%. A better measure here would be something called the geometric mean. Instead of summing all the values and dividing by the total number of values, as we do with the arithmetic mean, with the geometric mean we multiply those values together and then take their root. If there’s two numbers, we take the square root. If there’s three numbers, we take the cube root, and so on. So, if we take the geometric mean of those two values, we get the following:
p = √.015 * .0005 = .003 = .3%
We can then perform those calculations for each cell in the table corresponding to the combinations we found in our sample, shown below.
Probability of 50% Source Sound Match for Each Sound Combination
| Source | Target | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 5.3% | ||||
| 2 | 10.0% | 14.3% | 18.0% | ||
| 3 | 1.7% | 3.4% | 5.2% | ||
| 4 | 0.3% | 0.8% | 1.5% | ||
| 5 | 0.3% | 0.6% | |||
Now, if you thought (or were hoping) we were done, we’re not. We still have to take into account those 14% of sounds that were similar but not perfect matches. Thankfully we can take care of that using a similar process. For each cell in the table, we can also calculate the probability that, for a given number of sounds, there would be about half that would match AND another sound that would be similar. As you can see in the first table, the highest number of similar sounds in the target associated with a sound in the source is two (e.g., p and kw in the target associated with the sound b in the source), so our calculations assume that the probability of getting a similar sound is 2/19. We’ll use the same example of four sounds in both the source and target to get a sense of what that looks like:
(1/19) (1/19) (2/19) (16/19)
p = (.053) * (.053) * (.106) * (.842) = .00025
In this case there are 12 different combinations, so the overall probability is 12*.00025 or p = .003.
Once we make that calculation, we can use geometric means to get the probability of that happening around 14% of the time. I used the fraction of 1/6, or about 17%, which makes up for dropping the 4% from the perfect match earlier, with the other 5/6ths representing the probability of just 2 of the 4 sounds matching (.015), like so:
p = ![]() = .011 = 1.1%
= .011 = 1.1%
If we follow that same (labor intensive) process for each cell in the table, we get the following adjusted values.
Match Probabilities Adjusted for Similar-But-Not-Perfect Matches
| Source | Target | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 5.3% | ||||
| 2 | 7.0% | 11.0% | 14.7% | ||
| 3 | 1.4% | 2.0% | 4.0% | ||
| 4 | 0.3% | 0.4% | 1.1% | ||
| 5 | 0.2% | 0.4% | |||
So, after all that work, we have two important sets of estimates: 1) the probability that a given word will have a certain number of sounds associated with it in both the source and target language, and 2) the probability that each set of source/target sound combination will match to the extent seen in Stubbs’ data. We can then multiply the values in the two corresponding tables together to get the probability that 1 AND 2 happen for each sound combination. Summing all of those resulting values gives us our magical number: the probability that any given word will produce a correspondence like the ones that Stubbs identifies, purely on the basis of chance: p = .03, or 3%. That means we’d expect 3% of all Uto-Aztecan words to match any other given language, which happens to be on the high end of the estimate used by Rogers.
But we don’t just have one Old World language. We have several. Stubbs divides up his correspondences into three main sections: Egyptian and two different varieties of Semitic, Semitic p (which corresponds to a more Aramaic influence, which would have been the Hebrew of Lehi and Nephi) and Semitic kw (which corresponds to a more Phoenician influence, presumably through the Mulekites, who would have probably travelled to the Americas on Phoenician vessels). Stubbs never references proto-Semitic the same way he does for Uto-Aztecan—he instead associates Uto-Aztecan words with specific Semitic languages like Aramaic or Akkadian. You might think this would greatly increase the odds of getting a match, but since these languages are all part of the same language family, they’re highly interconnected. Semitic and Egyptian themselves are not entirely unrelated, further muddying the waters. I don’t see any problem with being a bit conservative, treating it as if Stubbs were trying to find connections with three independent Old World languages, and thus with three independent 3% chances to find a match with Uto-Aztecan. That probability turns out to be .087 (calculated by the formula 1 – (1 – 0.3)3), or an 8.7% chance of finding a match with any one of those three Old World languages, based on chance alone.
But what about Uto-Aztecan? Doesn’t the fact that there are 61 different languages in that family increase the odds of finding a match? Well, it does and it doesn’t. For one, each of those languages is obviously related as well. If we look at Stubbs’ correspondences, oftentimes the Egyptian or Semitic word is clearly related to words from many Uto-Aztecan languages—an average of 5.4, by my count. With that level of inter-relatedness, it’d be the equivalent of around 11 independent languages, rather than 61. Also, it’s pretty rare for Stubbs to cherry-pick words from individual languages. Based on my sample, around 75% of the time he’s using the entry for the base proto-Uto-Aztecan word, as detailed in his own much-praised vocabulary of Uto-Aztecan. Rather than assume that he can pull willy-nilly from all 61 languages (as do Rogers and Hansen), for our purposes it will be much cleaner to just exclude all the entries based on connections to specific individual languages.
In fact, we’re going to be doing quite a bit of excluding from Stubbs complete set of 1,528. First, Stubbs admittedly took a rather exploratory approach to these correspondences—he cast a broad net and wrote up everything he felt could conceivably be a connection, leaving the work of sorting through those possibilities to future scholars. This means that though some of his words are very close matches in terms of their meaning (e.g., #143, which has the meaning of pregnant in both languages) and others are pretty close (e.g., #77, which means red in Hebrew and brown in Uto-Aztecan), there are quite a few that are only tangentially related (e.g., #304, which means inhale or smell in Egyptian but cheek or mouth in Uto-Aztecan). As part of going through my sample, I made judgments as to how closely the meaning of the words in each language matched, and you can find a summary of that in the table below:
Number and Proportion of Meaning Matches
| Match Type | N | % |
|---|---|---|
| Exact (or near-exact) | 93 | 46.0% |
| Close | 72 | 35.6% |
| Distant | 35 | 17.3% |
Providing that kind of leeway in meaning dramatically increases the likelihood of finding a false match, because you’re not just trying to match a single word anymore. For the matches that are close but not exact, you get to roll the dice again for each synonym in the set. For more distantly related matches, you’re rolling it as often as your imagination and creativity allow. I don’t think Stubbs necessarily went amiss with his approach, since we would want this sort of initial effort to explore all the available possibilities. But it does mean that we’ll have to exclude at least some of the ones where flexibility was applied in terms of meaning.
From there, we have a couple options for how to proceed. We could just exclude the more distant ones, or we could rely on only the ones that have exact or nearly exact matches. Including the close matches would mean trying to figure out how many synonyms we’d expect to find on average for each word in Uto-Aztecan. I did make an attempt at this, sampling from Webster’s online thesaurus to get a sense of how many synonyms words might have. Based on a random sampling of 20 words from the table in the appendix, there’s an average 7 such synonyms in English. But English is a very different beast than Uto-Aztecan—Webster’s dictionary has over 400,000 words in it, accumulated over centuries of contact with Latin, Germanic, and Scandinavian languages, while Stubbs’ vocabulary for Uto-Aztecan only has 2,700 entries. Since I don’t think anyone has bothered to put together a good thesaurus for Uto-Aztecan, we’re probably up a creek in terms of trying to estimate the average number of synonyms. So that leaves us to consider just the exact matches.
Lastly, we need to deal with the possibility that Stubbs just plain got his correspondences wrong—that his misreading of Uto-Aztecan languages led him to see correspondences that weren’t actually there. Hansen raises 14 of these possibilities in his critical review, possibilities that Stubbs attempted to counter in his response. I don’t have the expertise to be able to judge between those arguments, and there may be only a handful of people in the world that do have the expertise. Trying to account for Stubbs’ possible errors is tricky, since Hansen obviously didn’t conduct a complete review or even a systematic one—there could be many more issues hiding behind the ones he brought up, or it could be that those are all the issues he was ever going to see. In my mind, the only fair way to treat the issue is to accept Stubbs’ apparently honest assessment—that 12 of the 14 correspondences continue to hold up despite Hansen’s objections (around 85%). We’ll make a conservative adjustment here, handicapping Stubbs by counting only 80% of those correspondences as valid.
HEY: If you skipped the above due to excessive mathiness, you can start paying attention again.
All told, based on my sample, and after excluding correspondences that draw from individual Uto-Aztecan languages and adjusting for an assumed 20% error rate on the part of Stubbs, that leaves us with an estimated set of 422 with exact or near exact meaning matches out of the original 1,528. You can get a more visual sense of how I arrived at that number below:
 Note: Values are estimates based on sample data.
Note: Values are estimates based on sample data.
If that’s the number of solid matches we observe in Stubbs’ data, how many would we expect to appear due to chance? Well, if we apply our earlier estimate of an 8.7% chance correspondence rate to Stubbs’ entire compendium of 2,700 Uto-Aztecan words, we would expect 235, which means Stubbs has found a little less than double the correspondences that we’d expect on the basis of chance. That alone should suggest that the evidence Stubbs has gathered is unexpected. How unexpected, exactly? Well, if we throw those numbers into a chi-square (detailed in the table below), the result is fairly eye-popping, with χ2(1) = 60.6, p = 6.99 x 10-15. At long last, we now have our consequent probability estimate.
Chi-Square Values Comparing Stubbs’ Collection with Chance Correspondences
| Observed (Expected) [Chi-Square Value] |
Chance Correspondences | Stubbs’ Collection |
|---|---|---|
| Match | 235 (328.5) [26.6] | 422 (328.5) [26.6] |
| Non-Match | 2,465 (2,371.5) [3.69] | 2,278 (2,371.5) [3.69] |
Posterior Probability
PH = Prior Probability of the Hypothesis (our initial estimate of the likelihood of an authentic Book of Mormon, based on the evidence we’ve considered thus far, or p = 1 — 2.07 x 10-19)
CH = Consequent Probability of the Hypothesis (our estimate of the likelihood of observing correspondences like these if the Book of Mormon is authentic, or p = 1)
PA = Prior Probability of the Alternate Hypothesis (our initial estimate of the likelihood of a fraudulent Book of Mormon, or 2.07 x 10-19)
CA = Consequent Probability of the Alternate Hypothesis (our estimate of how likely we would be to observe correspondences like these by chance, or p = 6.99 x 10-15)
PostProb = Posterior Probability (our new estimate of the likelihood of an authentic Book of Mormon)
| PH = 1 — 2.07 x 10-19 | |
| PostProb = | PH * CH |
| (PH * CH) + (PA * CA) | |
| PostProb = | (1 — 2.07 x 10-19 * 1) |
| ((1 — 2.07 x 10-19) * 1) + (2.07 x 10-19 * 6.99 x 10-15) | |
| PostProb = | 1 — 1.44 x 10-33 |
Lmag = Likelihood Magnitude (an estimate of the number of orders of magnitude that the probability will shift, due to the evidence)
Lmag = log10(CH/CA)
Lmag = log10(1 / 6.99 x 10-15)
Lmag = log10(1.43 x 1014)
Lmag = 14
Conclusion
Stubbs’ work should clearly not be easy to dismiss or dispense with. People can pick at individual correspondences as much as they like, but as a collection they appear to be quite formidable, and unexpected enough to earn a solid third place spot in our canon of positive evidence. On the other hand, the critics are certainly correct that we should expect a considerable number of correspondences on the basis of chance—just not nearly as many as Stubbs has been able to accrue. Shaving his set of over 1,500 down to the most exacting entries reveals a solid core that chance alone can’t quite match.
Skeptic’s Corner
Despite having slaved over this analysis more than any other, I’d be more than happy for someone else to come along and show me the error of my ways, and I can see quite a few places where they just might be able to do so. The first and most obvious one is that samples do not equal populations—it’s quite possible that a complete accounting of Stubbs’ correspondences could dramatically alter these estimates. The second is that the probability of sound matching isn’t going to be quite 1/19, because some sounds are more common than others. If more common sounds have a higher probability of matching then my match probability estimates would be systematically too low. This doesn’t appear to be the case, with the correlation between frequency and match probability not reaching significance (r = .19, p = .44), but a good simulation study would be the only way to know for sure.
The third is my assumed error rate. With Stubbs in control of both the Uto-Aztecan correspondences and the Uto-Aztecan dictionary he’s comparing it to, it’s possible that he (perhaps unconsciously) shaped entries in the dictionary to match the correspondences he thought he saw in the source languages. If so, then a bunch of other Uto-Aztecan experts could look closely at these matches and be able to point out where he was mistaken. So far Hansen is the only one to do so, and Stubbs appears to have argued well for his positions. Based on my analysis here, he would’ve had to have made substantial errors in over half of the correspondences to match what we’d expect on the basis of chance.
Lastly, as I’ve mentioned before, chi-square tests are notoriously sensitive to sample size, and Stubbs’ sample size is definitely enough to qualify as large. The best way to address that concern would be to do an inventory of chance matches in other languages, and see what chance is actually able to produce out in the wild. We could then compare the values from this analysis with the distribution of chance matches in unrelated languages, and see how far outside that distribution Stubbs’ work falls. If comparisons like the ones made by Stubbs fall close to what I’ve calculated here, though, then the critics are in a bit of a pickle, and Stubbs really has uncovered some of the most convincing evidence available for an authentic Book of Mormon.
Next Time, in Episode 20:
When next we meet, we’ll consider the charge that Joseph plagiarized Book of Mormon place names from the (very wide) area around Palmyra.
Questions, ideas, and infectious diseases can be planted on high-touch surfaces within BayesianBoM@gmail.com or submitted as comments below.
Appendix
| English Meaning | Meaning Match | Num of UA Lang | Source | Target | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Language | Word | Meaning | Sounds | S1 | S2 | S3 | S4 | S5 | Language | Word | Meaning | Sounds | S1 | S2 | S3 | S4 | S5 | |||
| Plural suffix | Exact | 10 | Hebrew | -iima | plural suffix | 1 | -m- | UA | -ima | plural suffix | 1 | -m- | ||||||||
| Sit | Exact | 5 | Hebrew | ysb | sit, dwell | 3 | y | s | b | UA | yasipa | sit, reside | 3 | y | s | p | ||||
| Gleam | Close | 1 | Arabic | snw | gleam, shine | 3 | s | n | w | Hopi | soniwa | beautiful, bright | 3 | s | n | w | ||||
| Earth | Close | 10 | Arabic | barr- | uncultivated ground | 3 | b | r | — | UA | kwiya | earth | 3 | kw | r | a | ||||
| Worm | Exact | 4 | Syriac | biltii | boring worm-the | 3 | b | l | t | UA | kwici | worm | 2 | kw | c | — | ||||
| Well | Distant | 1 | Hebrew | be’or | pit, well | 3 | b | ‘o | r | SP | kwi’oC | hollow and round | 3 | kw | ‘o | C | ||||
| Woman | Close | 1 | Hebrew | bahuuraa | young woman | 3 | b | h | r | Sh | kwihi | wife | 2 | kw | h | |||||
| Take | Exact | 9 | Arabic | -qbid | take, carry | 3 | q | b | d | UA | kwisiC | take, carry | 3 | kw | s | C | ||||
| Go | Exact | 13 | Arabic | mrr | pass, go, walk | 2 | m | r | r | UA | miya | go | 2 | m | y | — | ||||
| Say | Exact | 6 | Hebrew | ‘aamar | say | 3 | ‘ | m | r | UA | umay | say | 3 | u | m | y | ||||
| Red | Close | 6 | Hebrew | ‘dm | be red | 3 | ‘ | — | d | m | UA | oNtam | brown | 4 | o | N | t | m | ||
| Yell | Close | 1 | Hebrew | srh | cry, roar | 3 | s | r | h | UA | cayaw | yell | 3 | c | y | w | ||||
| Grow old (of women) | Exact | 9 | Arabic | ʔagaza | grow old (of women) | 3 | ʔ | g | z | Tr | wegaca | grow old (of women) | 3 | w | g | c | ||||
| Hair | Exact | 11 | Hebrew | seeʔaar | hair | 3 | s | ʔ | r | UA | suwi | body hair | 2 | s | w | — | ||||
| Head | Exact | 5 | Hebrew | roos | head | 2 | r | s | UA | toCci | head | 2 | t | c | ||||||
| Plural prounoun | Close | 6 | Semitic | -kVm | plural pronoun | 2 | k | m | UA | ‘im | plural suffix | 2 | ‘ | m | ||||||
| Fellow | Distant | 5 | Egyptian | snw | companion, fellow, equal | 3 | s | n | w | UA | sinu | another, different | 2 | s | n | — | ||||
| Pregnant | Exact | 8 | Egyptian | bk’ | pregnant | 3 | b | k | ‘ | UA | poka | stomach, pregnant | 3 | p | k | a | ||||
| Wrap | Close | 3 | Egyptian | t’yt | shroud | 4 | t | ‘ | y | t | UA | tawayi | wrap around | 3 | t | w | y | — | ||
| Earth | Close | 5 | Egyptian | t’ | earth, land, ground | 2 | t | ‘ | UA | ta’V | sand, dust | 2 | t | ‘ | ||||||
| Festive | Distant | 6 | Egyptian | hbi | be festive | 3 | h | b | i | UA | hupiya | sing, song | 3 | h | p | y | ||||
| Hew | Distant | 1 | Egyptian | wh’ | hew (stone) | 3 | w | h | ‘ | Hopi | waho(-k-) | spill particulate matter | 3 | w | h | k | ||||
| Stink | Exact | 14 | Egyptian | hw’ | foul, offensive, stink | 3 | h | w | ‘ | UA | hu’a | break wind, stink | 3 | h | u | ‘a | ||||
| No, negative | Exact | 2 | Egyptian | tm | negative, no | 2 | t | — | m | WTr | ta’me | no, negative | 3 | t | ‘ | m | ||||
| Close (mouth) | Exact | 11 | Egyptian | tm | close (mouth) | 2 | t | m | — | UA | timam | to close | 3 | t | m | m | ||||
| Desert | Distant | 2 | Egyptian | thn | shine, gleam | 3 | t | h | n | UA | tohono | desert, plain | 3 | t | h | n | ||||
| Sandal | Exact | 6 | Egyptian | twt | sandal, sole of foot | 3 | t | w | t | UA | tuti | sandals | 3 | t | u | t | ||||
| Shoe | Close | 4 | Egyptian | tbt | sandal, sole | 3 | t | b | t | UA | poca | shoes | 2 | b | c | |||||
| Heart | Exact | 1 | Egyptian | ib | heart, centre | 2 | i | b | — | — | TO | iibdag | heart, inner life | 4 | i | b | d | g | ||
| Capable | Close | 5 | Egyptian | iqr | capable, efficient | 3 | i | q | r | UA | yikar | knowing, able, good | 3 | y | k | r | ||||
| Wrap | Exact | 9 | Egyptian | wt | wrap in | 2 | w | t | UA | witta | tie, wrap | 2 | w | t | ||||||
| Like | Exact | 2 | Egyptian | mwy | watery | 3 | m | w | y | UA | muwa/i | wet | 3 | m | w | i | ||||
| Follow | Close | 15 | Egyptian | i-mr | want, follow me | 3 | i | m | r | UA | miri | run, flow, go, want | 2 | — | m | r | ||||
| Father | Distant | 5 | Egyptian | msi | bear, give birth, be born, create | 3 | m | s | i | UA | masi | father | 3 | m | s | i | ||||
| Voice | Distant | 1 | Egyptian | xr | speak to, voice | 2 | x | r | Ls | kara/i | belch, croak, ring | 2 | k | r | ||||||
| Fruit | Exact | 14 | Egyptian | dqr | fruit | 3 | d | q | r | UA | taka(C) | fruit | 3 | t | k | C | ||||
| Hill | Close | 3 | Egyptian | dhnt | mountain top | 4 | d | h | n | t | UA | ton(n)oC | hill | 3 | t | — | n | C | ||
| Hot | Exact | 4 | Egyptian | t’w | hot, heat, be hot, (glow) of fire) | 3 | t | ‘ | w | UA | tu’i | hot | 2 | t | ‘ | — | ||||
| Thigh | Exact | 10 | Egyptian | xps | foreleg, thigh | 3 | x | p | s | UA | kapsi | thigh | 3 | k | p | s | ||||
| Left | Exact | 3 | Egyptian | i’bty | left, east | 5 | i | ‘ | b | t | y | UA | opoti | left | 4 | — | o | p | t | y |
| Mouth | Distant | 13 | Egyptian | xnm | inhale, smell | 3 | x | n | m | UA | kaCma | cheek, mouth | 3 | k | C | m | ||||
| Forget | Exact | 11 | Egyptian | smx | forget, neglect | 3 | s | m | x | UA | suma | forget | 2 | s | m | — | ||||
| Yellow | Exact | 1 | Egyptian | qny | be yellow | 3 | q | n | y | Cp | kenekene’e | yellow | 4 | k | n | k | n | |||
| Go round | Close | 9 | Egyptian | qd | go round, turn | 2 | q | d | UA | koti | stir, mix | 2 | k | t | ||||||
| Pot | Close | 2 | Egyptian | qd | pot | 2 | — | q | d | UA | tikori | dish, plate, bowl | 3 | t | k | r | ||||
| Four | Exact | 14 | Egyptian | ifdw | four | 4 | i | f | d | w | UA | wattiwi | four | 4 | w | t | t | w | ||
| Climb | Exact | 1 | Egyptian | hfd | climb | 3 | h | f | d | UA | hu(w)at | climb, rise | 3 | h | w | t | ||||
| Neck | Close | 1 | Egyptian | ts | neck | 2 | t | s | — | CN | toski-tl | throat, voice | 3 | t | sk | tl | ||||
| Finish | Exact | 2 | Egyptian | grh | complete, finish off | 3 | g | r | h | Tr | gare | be able, finish | 2 | g | r | — | ||||
| Net | Exact | 3 | Egyptian | inqt | net | 4 | i | n | q | t | UA | ikkaC | carrying net | 3 | i | — | k | t | ||
| Near | Exact | 2 | Egyptian | tkn | be near, draw near | 3 | t | k | n | TSh | tikinaa | close to, near to | 3 | t | k | n | ||||
| Limp | Exact | 1 | Egyptian | gnn | weak, loose, limp | 3 | g | n | n | Eu | kanan | lame, limp, maimed | 3 | k | n | n | ||||
| Foot | Exact | 15 | Egyptian | rd | foot, leg | 2 | r | d | UA | tara | foot | 2 | t | r | ||||||
| Wine | Close | 1 | Egyptian | irp | wine | 3 | i | r | p | Ch(L) | iyaavi | wild grape | 3 | i | y | v | ||||
| Long legs | Distant | 1 | Egyptian | wr-rdw | great (of) legs | 5 | w | r | r | d | w | UA | wiC-talo | roadrunner | 4 | w | C | — | t | l |
| See | Close | 1 | Egyptian | nw | see | 2 | n | w | Tr | no- | to be visible | 2 | n | w | ||||||
| Remember | Close | 1 | Egyptian | ʔnx | be conscious of | 3 | ʔ | n | x | Ktn | winikai | remember | 3 | w | n | k | ||||
| Lame | Distant | 2 | Egyptian | nny | weary, lazy, lame | 3 | n | n | y | UA | nina | bad, useless | 2 | n | n | — | ||||
| Knife | Close | 7 | Egyptian | p’q | fine, thin, sheet of metal | 3 | p | ‘ | q | UA | pikkat | knife | 3 | p | k | t | ||||
| Lung | Close | 9 | Egyptian | sm’ | lung | 3 | s | m | ‘ | UA | sumaC | breathe | 3 | s | m | C | ||||
| Insect | Close | 15 | Egyptian | mht | an insect | 3 | m | h | t | UA | mCt | tick | 3 | m | C | t | ||||
| Together | Close | 3 | Egyptian | nʔw | to mate, press through | 3 | n | ʔ | w | UA | nawi | together with | 2 | n | — | w | ||||
| Pierce | Exact | 4 | Egyptian | tbs | pierce | 3 | t | b | s | UA | tapusa | pierce | 3 | t | p | s | ||||
| Eat | Close | 2 | Egyptian | eat | 2 | q | q | UA | koki | graze | 2 | k | k | |||||||
| Inhale | Distant | 3 | Egyptian | xnm | inhale, smell, eat | 3 | x | n | m | UA | kanmi | jackrabbit (the nibbler) | 3 | k | n | m | ||||
| Quail | Exact | 3 | Egyptian | p’ʔt | quail | 4 | — | p | ‘ | ʔ | t | UA | supa’awi | quail | 4 | s | p | ‘ | w | — |
| Command | Close | 3 | Egyptian | hn | order, command, delegate | 2 | h | n | UA | hura | send | 2 | h | r | ||||||
| Mourn | Close | 1 | Egyptian | h’i | mourn, wail | 3 | h | ‘ | i | — | Wr | ho’kewa | tears | 4 | h | ‘k | e | w | ||
| Sweep | Exact | 5 | Egyptian | ‘xi | sweep together | 3 | ‘ | x | i | — | UA | wak | sweep, comb | 2 | — | w | — | k | ||
| Weak (due to age) | Distant | 1 | Egyptian | nw | be weak (due to age) | 2 | n | w | Hopi | naawa | groan, moan | 2 | n | w | ||||||
| Reckon | Distant | 1 | Egyptian | ip | count, reckon | 2 | — | i | p | Cora | hihibe | read | 3 | hi | hi | b | ||||
| Solitude | Close | 2 | Hebrew | bad | solitude, except | 2 | b | d | UA | pari | one, different | 3 | p | r | ||||||
| Trust | Close | 2 | Hebrew | bth | trust | 2 | b | th | UA | cawa | believe | 2 | c | w | ||||||
| Pleasant | Close | 3 | Hebrew | bsr | sweet, pleasant | 3 | b | s | r | UA | pisa | like, love | 2 | p | s | — | ||||
| Swell | Exact | 4 | Hebrew | bsq | to swell | 3 | b | s | q | UA | posa | swell | 2 | p | s | — | ||||
| White | Exact | 1 | Hebrew | bws | be white | 2 | b | w | s | UA | pos | be white | 2 | p | — | s | ||||
| Cry | Exact | 1 | Hebrew | ti’bke | it cries | 3 | t | b | k | UA | taka | cry | 2 | t | — | k | ||||
| Look at | Exact | 7 | Hebrew | bbiit | look at | 2 | b | t | UA | pica | he looks | 2 | p | c | ||||||
| Lip | Exact | 1 | Hebrew | sapoot | lips | 3 | s | p | t | UA | puti | lip | 2 | — | p | t | ||||
| Person | Distant | 1 | Hebrew | ‘iis | man, person | 2 | i | s | Ca | is | person who does (verb) | 2 | i | s | ||||||
| Woman | Exact | 1 | Hebrew | ‘ist | woman, wife of | 4 | ‘ | i | s | t | Hp | wiiti | woman, wife | 3 | w | i | — | t | ||
| Come | Exact | 5 | Hebrew | ‘atii | come | 3 | ‘ | t | i | — | UA | wiic | come | 3 | w | — | i | c | ||
| Put on shirt | Exact | 1 | Hebrew | ‘pd | put on an ephod | 3 | ‘ | p | d | Tr | opata | put on a shirt | 3 | o | p | t | ||||
| Belt | Exact | 2 | Hebrew | ‘abnet | sash, girdle | 4 | ‘ | b | n | t | UA | natti | belt | 2 | — | — | n | t | ||
| Opponent | Exact | 3 | Akkadian | qardammu | enemy, opponent | 4 | q | r | d | m | UA | timmu | opponent | 2 | — | — | t | m | ||
| Sister | Exact | 9 | Aramaic | ‘axaat | sister the | 3 | ‘ | x | t | UA | wakati | younger sister | 3 | w | k | t | ||||
| Rock | Exact | 22 | Aramaic | riimaa | large stone | 2 | r | m | — | UA | timi-ta | rock | 3 | t | m | t | ||||
| Butt | Exact | 4 | Arabic | dubr | rump, backside | 3 | d | b | r | UA | tupur | hip, buttocks | 3 | t | p | r | ||||
| Grinding stone | Exact | 21 | Hebrew | maktes | grinding stone | 4 | m | k | t | s | UA | mattas | grinding stone | 3 | m | — | t | s | ||
| Beget | Close | 1 | Hebrew | zrʔ | bear a child | 3 | z | r | ʔ | CN | ciiwa | beget, gender | 2 | c | — | w | ||||
| Goo | Distant | 4 | Hebrew | psx | limp | 3 | p | s | k | UA | pisiC | goo | 3 | p | s | C | ||||
| Round | Exact | 7 | Hebrew | ʔagol | round | 3 | ʔ | g | l | UA | wakol | round(ed) | 3 | w | k | l | ||||
| Stork | Close | 3 | Arabic | laqlaq | stork | 4 | l | q | l | q | Ca | la’la’ | goose | 4 | l | ‘ | l | ‘ | ||
| Get up | Exact | 1 | Arabic | tlʔ | arise, come up | 3 | t | l | ʔ | — | Tb | tulu’ula | get up from sitting | 4 | t | l | ‘ | l | ||
| Bear a child | Exact | 1 | Hebrew | towlid | bear a child | 4 | t | w | l | d | Ls | lovli | bear a child, lay an egg | 3 | t | v | l | — | ||
| Drunk | Distant | 9 | Hebrew | nebel | skin bottle (of wine) | 3 | n | b | l | PUA | napai | alcoholic drink, drunk | 2 | n | p | — | ||||
| Drag | Exact | 3 | Hebrew | paraq | drag away, tear away | 3 | p | r | q | UA | piyok | pull, drag | 3 | p | y | k | ||||
| Arm | Exact | 9 | Aramaic | ‘eebaar-aa | limb, arm | 3 | ‘ | b | r | UA | pira | arm, right arm | 2 | — | p | r | ||||
| Game | Close | 1 | Hebrew | muusaad | game, what’s hunted | 3 | m | s | — | d | UA | musayid | buffalo, moose, elk | 4 | m | s | y | t | ||
| Hair | Close | 12 | Hebrew | semer | wool | 3 | s | m | r | UA | comya | hair | 3 | c | m | y | ||||
| Bright | Distant | 5 | Hebrew | shr | bright, clear | 3 | s | h | r | UA | cihari | sunrise, east, morning | 3 | c | h | r | ||||
| Five | Distant | 3 | Hebrew | ‘esbaʔ | finger, toe | 4 | ‘ | s | b | ʔ | UA | cipo | five | 2 | — | c | p | — | ||
| To be like | Exact | 3 | Hebrew | damaa | to be like, resemble | 2 | d | m | TO | -dima | to be like | 2 | d | m | ||||||
| Snow | Exact | 1 | Hebrew | seleg | snow | 3 | s | l | g | UA | sik | snow | 2 | s | — | k | ||||
| Push | Close | 3 | Hebrew | tqp | to overpower | 3 | t | q | p | UA | takipa | push, push many times | 3 | t | k | p | ||||
| Taste | Close | 10 | Hebrew | yo’kal | eat, feed, savor | 4 | y | ‘ | k | l | UA | yi’iki | swallow, taste | 3 | y | ‘ | k | |||
| God | Exact | 6 | Hebrew | Yahwe | Yaweh | 3 | y | h | w | UA | ya’wV | leader, diety | 3 | y | ‘ | w | ||||
| Laugh | Close | 11 | Hebrew | hattel | to mock | 3 | h | t | l | UA | ‘atti | laugh | 2 | ‘ | t | — | ||||
| Heavy | Distant | 25 | Syriac | pty | wide, enlarged | 3 | p | t | y | UA | petiy | be heavy | 3 | p | t | y | ||||
| Close eyes | Exact | 7 | Hebrew | ʔsm | to shut one’s eyes | 3 | ʔ | s | m | UA | cumma/i | close eyes | 3 | — | c | m | ||||
| Breathe | Exact | 12 | Hebrew | hippiis | breath, life, soul | 3 | h | p | s | UA | hikwis | breathe, spirit, heart | 3 | h | kw | s | ||||
| In | Exact | 10 | Hebrew | ba | in/at it | 1 | b | UA | -pa | at, in | 1 | p | ||||||||
| Heat | Distant | 6 | Hebrew | yhm | be in heat | 3 | y | h | m | UA | yu’mi | warm | 3 | y | ‘ | m | ||||
| Ankle | Exact | 2 | Syriac | qursel-aa | ankle bone | 4 | q | r | s | l | UA | koci | ankle(bone) | 2 | k | — | c | — | ||
| Tight | Distant | 2 | Hebrew | gadiis | heap of sheaves | 3 | g | d | s | UA | ngattas | tight | 3 | ng | t | s | ||||
| There is | Exact | 3 | Aramaic | ‘yt | there is/are | 3 | ‘ | y | t | Yq | kaita | there is | 2 | k | i | t | ||||
| Gnaw | Close | 3 | Hebrew | grm | gnaw or break, crush | 3 | g | r | m | Hp | ngaro | crunch down on | 2 | ng | r | — | ||||
| Dance | Close | 1 | Hebrew | gyl | circle, dance | 3 | g | y | l | Cp | ngayla | spin, twirl | 3 | ng | y | l | ||||
| Bow | Exact | 5 | Semitic | qast-o | bow-his | 3 | q | s | t | UA | gata | bow | 2 | g | — | t | ||||
| Belly | Exact | 2 | Arabic | kirs | stomach, paunch, belly | 3 | k | r | s | UA | kica | belly | 2 | k | — | c | ||||
| Dried | Close | 1 | Hebrew | qss | old, dried up | 2 | q | s | — | UA | koson | dry | 4 | k | s | n | ||||
| Chip | Distant | 1 | Syriac | qlp | peel, shell, scrape | 3 | q | l | p | Hp | haapo | get loosened | 3 | h | — | p | ||||
| Big | Distant | 7 | Hebrew | kabaaru | strong, mighty | 3 | k | b | r | UA | kapataC | long, tall | 4 | k | p | t | — | |||
| Straighten | Close | 12 | Hebrew | tqn | make straight | 3 | t | q | n | UA | tikaC | stretch/spread flat | 3 | t | k | C | ||||
| Daughter | Close | 12 | Arabic | mar’ | woman, wife, daughter, the | 3 | m | r | ‘ | UA | marCa | daughter, child, offspring | 3 | m | r | C | ||||
| Woman | Exact | 6 | Arabic | mar’a | woman, wife | 3 | m | r | ‘ | UA | mamma’u | woman, wife | 3 | m | m | ‘ | ||||
| Girdle | Close | 3 | Hebrew | hagor-taa | to gird, gird oneself | 4 | h | g | r | t | UA | wikosa | belt | 3 | w | k | s | — | ||
| Butterfly | Exact | 3 | Akkadian | gursiptu | butterfly | 5 | g | r | s | p | t | UA | asiNpu(tonki) | butterfly | 4 | — | — | s | p | t |
| Name | Exact | 12 | Arabic | dʔw | to call, name | 3 | d | ʔ | w | UA | tinwa | name | 3 | t | n | w | ||||
| Plow | Distant | 6 | Aramaic | paddaan | plow, yoke of oxen | 3 | p | d | n | UA | poto | digging stick | 2 | p | t | — | ||||
| Drink | Close | 26 | Hebrew | rwy | drink one’s fill | 3 | r | w | y | UA | hi’pa | drink | 3 | h | ‘ | p | ||||
| Storm | Close | 17 | Hebrew | suupat | storm, gale | 3 | s | p | t | UA | sipita | cold, cold wind | 3 | s | p | t | ||||
| Prevail | Close | 7 | Hebrew | tqp | overpower | 3 | t | q | p | UA | takopi | win in a game | 2 | — | k | p | ||||
| Leave | Exact | 3 | Syriac | sql | take, depart | 3 | s | q | l | UA | saka(la) | go, leave | 3 | s | k | ‘ | ||||
| Grind | Close | 20 | Hebrew | kts | pound fine | 3 | k | t | s | UA | tusu | grind | 2 | — | t | s | ||||
| Pound | Close | 2 | Hebrew | pss | break into pieces | 2 | p | s | UA | pisa | pound | 2 | p | s | ||||||
| Numb | Close | 5 | Hebrew | seleg-mukke | snow smitten | 5 | s | l | g | m | k | UA | sik-mukki | numb | 4 | s | — | k | m | k |
| Oak | Close | 2 | Arabic | gauza | nut | 2 | g | z | UA | kusi | oak, oak tree | 2 | k | s | ||||||
| His (suffix) | Close | 4 | Hebrew | -o | his | 1 | o | UA | -wa | possessed suffix | 1 | wa | ||||||||
| Set | Distant | 3 | Hebrew | moosiiʔ | set bed | 3 | m | s | ʔ | UA | mociwa | sit down | 3 | m | c | w | ||||
| Put | Distant | 6 | Hebrew | rby | shoot, throw | 3 | r | b | y | UA | tap | put | 2 | t | p | — | ||||
| Reed | Distant | 3 | Akkadian | ‘ebeh | reed, papyrus | 3 | ‘ | b | h | UA | wapi | foxtail | 2 | w | p | — | ||||
| Vision | Close | 3 | Hebrew | ro’eh | seer | 3 | r | ‘ | eh | UA | ti’a | experience a vision | 3 | t | ‘ | a | ||||
| Suck | Close | 11 | Hebrew | ynq | to suck | 3 | y | — | n | q | UA | yi’na | smoke by sucking | 3 | y | ‘ | n | — | ||
| Float | Exact | 2 | Syriac | qepa’ | float | 3 | q | p | ‘ | UA | qoppV | float | 3 | q | p | — | ||||
| Wide | Close | 7 | Aramaic | pth | wide open place | 3 | p | t | ‘ | UA | pitiwa | wide | 3 | p | t | w | ||||
| Spirit | Exact | 2 | Hebrew | ha-ruuh | spirit, wind | 3 | ha | r | h | UA | arewa | spirit | 3 | a | r | w | ||||
| Spit | Exact | 3 | Hebrew | roq | spittle | 2 | r | q | UA | cukV | spit | 2 | c | k | ||||||
| Breathe | Exact | 3 | Hebrew | hinnapes | breathe freely | 4 | h | n | p | s | UA | hiapsi | breathe | 3 | h | — | p | s | ||
| Footprint | Distant | 3 | Hebrew | ʔaaqeeb | heel, hoof, footprint | 3 | ʔ | q | b | UA | yiki | make, follow tracks | 2 | y | k | — | ||||
| Wood | Exact | 9 | Hebrew | ʔaab | item of wood | 2 | ʔ | b | — | UA | wopiN | wood | 3 | w | p | C | ||||
| Weasel | Exact | 2 | Syriac | silaas | weasel | 3 | s | l | s | — | UA | sisika | weasel | 3 | s | — | s | k | ||
| Willow | Distant | 6 | Hebrew | qaane | reed, stalk | 2 | q | n | UA | kana | willow | 2 | k | n | ||||||
| Worm | Close | 6 | Aramaic | ‘arqe-taa | fluke worm | 3 | ‘ | r | q | UA | wo’a | worm | 2 | w | ‘ | — | ||||
| Mud | Exact | 6 | Aramaic | sʔyn | mud-the | 5 | — | s | ʔ | y | n | UA | pa-sakwinaC | mud | 5 | p | s | kw | i | n |
| Bloom | Close | 14 | Hebrew | siih | bush | 2 | s | h | UA | si’aC | bloom, flower | 3 | s | ‘ | C | |||||
| Flower | Close | 6 | Hebrew | soosaan | lily | 3 | s | s | n | UA | soci | flower | 2 | s | c | |||||
| Cure | Exact | 6 | Hebrew | yurpa | to heal | 4 | y | r | p | ‘ | UA | yopa | cure | 2 | y | — | p | |||
| Lizard | Exact | 4 | Aramaic | yall-aa | lizard | 3 | y | l | ‘ | UA | yul | lizard | 3 | y | l | |||||
| Snow | Exact | 3 | Aramaic | talg-aa | snow-the | 3 | t | l | g | UA | takka | snow | 3 | t | — | k | ||||
| Footwear | Close | 2 | Aramaic | mooq-aa | felt-sock, stocking | 2 | m | q | UA | moko | footwear, shoe | 2 | m | k | ||||||
| Lion | Exact | 1 | Arabic | sibl | lion cub | 3 | s | b | l | Wr | sebori | baby mountain lion | 3 | s | b | r | ||||
| Effect | Distant | 1 | Hebrew | pʔl | to do, make accomplish | 3 | p | ʔ | l | — | Hp | powa-l-ti | cure, tame | 4 | p | w | l | t | ||
| Round | Exact | 1 | Hebrew | plk | round, spindle, circle | 3 | p | l | k | Hp | pola | round | 2 | p | l | — | ||||
| Afraid | Exact | 1 | Hebrew | yooger | to be afraid | 3 | y | g | r | Ca | yuki | to fear | 2 | y | k | — | ||||
| Watch | Close | 1 | Arabic | tbʔ | follow, trail | 3 | t | b | ʔ | Tr | tibu | watch, take care of | 2 | t | b | — | ||||
| Refuse | Close | 1 | Hebrew | m’n | refuse | 3 | m | ‘ | n | Hp | meewan | forbid, warn | 3 | m | w | n | ||||
| Shave | Close | 25 | Hebrew | sippaa | to make smooth | 2 | s | p | UA | sippa | scrape, shave, whittle | 2 | s | p | ||||||
| Open | Close | 3 | Arabic | pqh | to open the eyes, bloom | 3 | p | q | h | UA | paka | open | 2 | p | k | — | ||||
| Mother | Exact | 1 | Hebrew | ’em | mother | 2 | ‘ | m | Tb(H) | iimii | mother | 2 | i | m | ||||||
| Tied | Distant | 1 | Syriac | qewaayaa | loom, web | 3 | q | w | y | Ca | qaawi | get tied, hooked | 3 | q | w | — | ||||
| Sweep | Close | 5 | Aramaic | -kbod | to honor, sweep, look respectable | 3 | k | b | d | UA | poci | sweep | 2 | p | — | c | ||||
| Squirrel | Exact | 4 | Aramaic | simmora | squirrel | 3 | s | m | r | UA | cimo | squirrel | 2 | c | m | — | ||||
| Mud | Exact | 2 | Aramaic | hal-aa | mud-the | 3 | h | l | ‘ | UA | hala | moist/wet soil | 2 | h | l | — | ||||
| Good | Close | 4 | Syriac | atip | do good, treat well | 3 | ‘a | t | b | UA | atiip | good | 3 | a | t | p | ||||
| Bead | Distant | 1 | Herbrew | sor | flint | 2 | s | r | SP | coiC | bead | 2 | c | C | ||||||
| Thick | Close | 4 | Arabic | pgl | thick, soft, flacid | 3 | p | g | l | Hp | poongala | thick | 3 | p | ng | l | ||||
| Under | Exact | 5 | Hebrew | betaxat | in/at under | 4 | b | t | x | t | UA | pitaha | under | 3 | p | t | h | — | ||
| Opponent | Distant | 5 | Hebrew | bahuur | choose | 3 | b | h | r | UA | bihiri | expensive, opponent | 3 | b | h | r | ||||
| Middle | Exact | 2 | Hebrew | took | midst, middle | 2 | t | k | UA | tok | with, near, middle | 2 | t | k | ||||||
| If | Close | 1 | Arabic | idan | then, if, therefore, when | 3 | i | d | n | Tb(H) | tanni | if | 2 | — | t | n | ||||
| Bag | Close | 13 | Syriac | te-ʔre | contain, grip | 3 | t | ʔ | r | UA | tanga | bag | 2 | t | ng | — | ||||
| Rat | Close | 5 | Syriac | nedaal | fieldmouse | 3 | n | d | l | UA | tori | rat | 2 | — | t | r | ||||
| Man | Exact | 6 | Akkadian | awiil | man | 3 | a | w | l | Hopi | owi | male, man | 2 | o | w | — | ||||
| Evening | Exact | 2 | Hebrew | ʔaareb | become evening | 3 | ʔ | r | b | Wr | ari | late afternoon, become evening | 3 | — | r | — | ||||
| Bathe | Exact | 7 | Syriac | asiig | wash | 3 | a | s | g | UA | asi | bathe, swim | 2 | a | s | — | ||||
| Braid | Exact | 11 | Syriac | bkt | weave | 3 | b | k | t | UA | kwiCta | braid, wind around | 3 | kw | C | t | ||||
| Bite | Exact | 26 | Hebrew | qrs | bite | 3 | q | r | s | UA | ki’ca | bite | 3 | k | ‘ | c | ||||
| Come on | Close | 3 | Hebrew | haavaa | come on | 2 | h | v | Kw | ‘iivi | now, go ahead | 2 | ‘ | v | ||||||
| Knee | Exact | 19 | Arabic | rukbat | knee | 4 | r | k | b | t | UA | tonga | knee | 2 | t | ng | — | — | ||
| Big | Exact | 1 | Hebrew | mugdal | big | 4 | m | g | d | l | Ls | muka-t | big, large | 3 | m | k | — | t | ||
| Perfect tense prefix | Exact | 2 | Hebrew | -wa | perfect tense marker | 1 | wa | UA | -wa | perfect tense marker | 1 | wa | ||||||||
| Mix | Close | 3 | Hebrew | ʔrb | be mixed up with | 3 | ʔ | r | b | UA | na-‘rowa | stir, mix | 3 | ‘ | r | w | ||||
| Comfort | Distant | 1 | Hebrew | sly | have rest, be at ease | 3 | s | l | y | — | Hp | salayti | become gratified, fulfilled, pleased | 4 | s | l | y | t | ||
| Person | Distant | 7 | Hebrew | yo(w)liid | begetter, father | 4 | y | w | l | d | UA | yori | Person | 2 | y | — | r | m | ||
| Catch | Close | 1 | Hebrew | qaamit | seize | 3 | q | m | t | UA | kamiic | to catch | 3 | k | m | c | ||||
| Louse | Close | 1 | Syriac | sa’p-aa | crawling locust | 3 | s | ‘ | p | — | Ktn | sivacici | body louse | 4 | s | v | c | c | ||
| Rub | Close | 1 | Aramaic | swp | smooth, rub, polish | 3 | s | w | p | Ktn | suvi’ | to rub clothes | 3 | s | v | ‘ | ||||
| Trembling | Close | 1 | Syriac | srd | to quake, be terrified | 3 | s | r | d | Ktn | sariri | trembling | 3 | s | r | r | ||||
| Testicle | Exact | 9 | Egyptian | isnwi | testicles | 4 | i | s | n | w | UA | noyo | egg, testicle | 2 | — | — | n | y | ||



Kyler, I’m impressed with your statistical skills. I was a math major before going into languages / linguistics, but that was 50 years ago, so I have forgotten most of it. I’m thinking to have a lot of probability stats in my next book on UA (after I brush up on probabilities). You’d be good to check me on it, or maybe I should hire you to do it. By the way, I grew up with a Rasmussen family in my Provo PVIII ward, northeast Provo just west of the temple; Karen Rasmussen was my age. Can’t remember the father’s first name. Any relation do you think? I’ll try to answer some of your questions briefly, as my brain loses increasing degrees of clarity the further past my bedtime. As for unusual semantic combinations like ‘snake, twin’ there are perhaps a dozen other semantic combinations that are unusual yet carry over into UA, found so far.
Let me explain the 1 in a trillion probability for the Tarahumara (Tr) revelation. UAnists have noticed for a century that Proto-UA initial *t- (at beginning of a word) appears as r- in Tr. But that’s all they ever say. They don’t mention that sometimes Tr keeps t- to correspond to PUA *t and it does not change to r. (This all has to do with initial position.) No one could explain why some change to r- while others remain t-. But the Semitic and Egyptian data clarify it. What happened is that Sem and Eg r- changed to t- at the beginning of the word, so that it merged with UA *t-, which comes from Sem / Eg t and d. So initial r, t, d all became *t- in all the other UA langs. Then we have the Tr data of about 40 cognates in Tr that correspond to initial *t-, but interestingly the half that correspond to a Sem or Eg word beginning with r, show Tr r-, and the other half that correspond to a Sem or Eg word beginning with t or d, which rightly becomes PUA *t, remain t- in Tr. So for those knowing nothing of that underlying explanation, they would look at each initial Tr t and the chance of whether it matches underlying t- / d- or whether underlying r-, is a toss of a coin, no? The chance that it would match Sem / Eg or not match is 50/50, if one knows not. So guessing right on the first is 50/50, then guessing right also on the 2nd or 2 in a row, is 1/4 and so on. So it seems to me it’s like tossing a coin 40 times and the probability of guessing right 40 times in a row. Or that for 40 in a row to match the Sem/Eg by chance is 1 over 2 multiplied 40 times, or ½ to the 40th power, no? which is 1 / 1,099,511,627,776, slightly less than 1 in a trillion, if I multiplied correctly. If the probability is something different, what am I misfiguring? But my brain is brain-dead this time of night. It might do better in the morning. I do appreciate your approach—the statistical analyses applied to my work—because that is exactly what I’ve long thought needs to happen more often in comparative work. The linguistic comparative method is used to find what “seems” probable or improbable, in a general sense to linguists’ general judgment, but they seldom apply the math to figure actual probabilities of it all. Very good. Let’s stay in touch.
Thanks for the more detailed explanation. Now that you’ve laid it out, what you’re describing, if it lines up perfectly for all 40 cognates, would indeed be equivalent to 40 correctly guessed coinflips. That sounds like great material for a brief Interpreter article laying that evidence out, and the mathematical argument would be an important part of that.
Between the Tr evidence and the dozen semantic pairings, that would certainly have been enough to push this evidence into Critical Strike territory, and would’ve landed UA as the second strongest piece of evidence in the corpus, behind EModE (which I handicapped to a greater degree than I’ve done for UA). I regret not thinking those issues through in my essay, but if I ever get another chance to frame the UA evidence those will definitely be incorporated.
I’m always happy to assist when it comes to reviewing and thinking through these sorts of arguments, so feel free to reach out anytime.
As for whether I’m related to Rasmussens in Provo, the answer to that is a definite probably, though it’s likely distant, and I wouldn’t be able to trace the geneology. Those Danes got around, so you tend to find Rasmussens all over.
Thank you Kyler. You did a tremendous amount of work. I’ll add one more thought, Yes, speaking of the 3 languages found in UA (Hebrew, Aramaic, Egyptian), Rogers and an echo from Jonathan Green suggested that with so much to choose from, it would seem “impossible not to find cognates.” However, early in my career I looked for Hebrew / Aramaic / Semitic or Egyptian in several language families (each with a few to dozens of languages): Athapaskan, Yuman, Pomoan, Wintuan, Maiduan, Shastan, Yana, Kiowa-Tanoan, Keresan, Zuni, Salishan, Karuk, Algic, Siouan, Caddoan, Iroquoian, Muskogean, and Uto-Aztecan in North America; and Mayan, Totonacan, Mixe-Zoquean, Otomanguean, and a few isolates in Central America; and Chibchan, Cariban, Tupian, Paez, Arawakan, Aymaran, Witotoan, Quechuan, Matacoan, Pano-Tacanan, Guahiboan, Barbacoan, Macro-Je, Jivaroan, Movima, Zaparoan, and others in South America, but I did not find such an array of similarities in dozens of other language families, like I found in Uto-Aztecan, so then I specialized in UA. If I were prone to imagine or see what was not there, it would have happened long before UA.
Nor was any such list of Egyptian cognates found in those other hundreds of languages or 30-40 language families. Critics also need to keep in mind that each category has 400 or more items. Many language families are founded on 150 cognate sets or less. So consider each of the 3 separately and each one (400 plus) is a case all its own, regardless the other two. I am hoping that Times and Seasons will let me publish a post to clarify oversights in Jonathan Green’s post of Jan 2019. I have a post prepared, but they have not responded yet.
Thanks for the comment Brian. Your initial failed search for correspondences in these additional language families is definitely food for thought. Though I’m sure it’s tough to cast your mind back that many years previous, it’d be interesting to know how many words you looked through in each language family and if you stumbled upon any chance correspondences that you decided weren’t meaningful enough for further investigation. It’s possible that my estimate of 8.7% is too high, and doesn’t reflect the practical exercise of searching for correspondences (e.g., where you might have had more stringent mental criteria for inclusion at the start of your search, and then followed up within Uto-Aztecan with a broader exploratory net). Robust systematic data directly comparing your Uto-Aztecan effort with what we’d expect due to chance from other language families is exactly the kind of analysis that would put the issue to bed, at least within my own mind.
I can’t express enough my gratitude for your work in this space, and I look forward to seeing you continue to blaze this trail.
Thank you Kyle and all. Impressive. Yes, many particulars or details keep turning up to strengthen the case. While modern English retains only 15% of the Old English vocabulary and Yiddish shows a similarly low percentage of Semitic, the UA vocabulary may be 35-40% from the Semitic and Egyptian components (double the other two), and in the pervasive cognates (that are in 25 or more of the 30 UA languages) it is 60% (Exploring, pp. 344-5). And only 11 UA cognates appear in all 30 UA languages and 11/11 or 100% of those are of the Semitic-Egyptian data.
The probabilities of many aspects are tremendously in its favor. For example, semantic combinations, like Egyptian ‘serpent, partner’ to UA ‘snake, twin’ (Exploring, number 332; Changes in Languages, p. 68). What is the chance that two meanings so different (serpent and partner?) would also be found in the corresponding UA word, which also means ‘snake, twin’? And there are many more. Most impressive is that nine unanswered phonological questions in UA have never been explained in the 100 years since the language family was demonstrated by Edward Sapir in two articles (1913, 1915). Then after the underlying Semitic and Egyptian component is found, the Semitic-Egyptian data explain seven of the nine (Exploring, pp. 306-322; “Answering” number 23). That is astounding! For example, one of those is the solution to why Tarahumara reflects UA *t- as both r- and t-, about half in each category for some 40 items. Curiously, the previously unexplained variation matches Semitic and Egyptian r- vs. t-/d-! The probability of that by chance is less than 1 in a trillion (1/2 multiplied to the 40th power). That kind of explanatory power is impossible, unless the case is valid. As mentioned by Kyle, the Interpreter article “Answering the Critics in 44 Rebuttal Points” answers many questions.
brian stubbs
Thanks Brian. The issue of semantic combinations is very interesting and would indeed serve to further reduce the role of chance in producing those correspondences. If my estimates here are worth anything, you’d have to consider the probability of a word in both the source and target languages having at least two apparently unrelated meanings (I don’t see any in a cursory review of my sample, so my guess is that it would be low, at perhaps 1%), and then to have the sound correspondences match (8.7%), and the secondary meaning match (perhaps 10%, based on my onomatic analysis). Putting those three together, that would put the probability of that happening with any given PUA word at 8.7 x 10^-6. The probability of getting even one of those in the corpus of 2700 PUA words would be p = .02, and finding more than one would be exponentially less likely.
I’m a little less sure about your 1 in a trillion estimate for solving the issue with Tarahumara. It sounds like you’re treating it as if the odds of the connections providing that solution were equivalent to getting a string of coin flips right 40 times over. That might apply if the problem was having a set of 40 words that would normally vary with half r- and half t- somehow come up all r-‘s. You can correct me if I’m mistaken, but I don’t think that quite captures the issue at hand.
Another way to frame that probability would be to consider: 1) the probability of at least one language in a family showing systematic variation where the sounds wouldn’t appear to derive naturally from the base language, and 2) the probability that comparison languages would show that same sound variation. I have no idea what the probabilities would be in each case, and they’re probably low, but I don’t see a case for it amounting to 1 in a trillion. I also wonder why we only see that sound variation in Tarahumara rather than in a greater array of UA languages (if that’s indeed the case). It would definitely be interesting to dig into a more in-depth analysis on this topic.
Cheers!
Thanks for the article, it was certainly interesting. By any chance is Stubbs’ work in the middle of peer review or is going to be peer reviewed soon? It seems to me that that would be the best possible oppurtunity to change the scientific consensus for that to happen. Also, another significant aspect of Stubbs’ work would be that if it were validated to become part of the scholarly consensus, it would essentially make the DNA question moot as it would show that a lack of middle eastern DNA among current native american populations would be almost irrelevant as it would already be proven that there was Middle-Eastern contact with pre-columbian America. In other words, one of the most important (in my opinion) criticisms of The Book of Mormon (that being the DNA controversy) would be essentially dead. Not to mention, problems having to do with a lack of Egyptian or Hebraic writing or whatever could arguably become moot as well, after all, a lack of found middle eastern writings would no longer be as relevant as evidence against The Book of Mormon because we would already know that there were in fact middle easterners in contact with Pre-Columbian America so it would only then be question of did those people leave writings, but not a question of whether or not they were there in the first place. In my opinion, the relevance of Stubbs’ work (if it becomes the scholarly consensus) cannot be understated.
Jeremy,
Note the sentence in the episode, above, that states “Stubbs has since responded to both Rogers and Hansen in-depth in this article.” You’ll want to read the article, as it provides answers to some of your questions. For instance, the question about peer review is addressed, specifically, in point 40 and DNA is addressed in point 27.
I hope that helps, and good luck with your studies.
-Allen
Thanks for pointing these out, Allen, and thanks to Jeremy for his thoughts.
I wish Stubbs point about HLAs (and their implications for hereditary admixture between the Semitic and Uto-Aztecan peoples) had sunk into my brain more before I put together my DNA essay. I’d be interested in someone like Ugo’s thoughts on the matter, but I’m with Stubbs that the correspondence is striking.
And it’s clear to me from point 40 that Stubbs has done his level-best to get his book in front of the eyes of his peers, and that the initial reactions are very promising (a Harvard scholar working in linguistics and Mayan anthropology saying “It is the most interesting and significant piece of research I have seen in years.” should get anyone’s heart pumping). I idly wonder a bit, though, why he hasn’t worked on submitting a summary article to a mainstream journal. I suspect it’s because the strength of his argument lies in the breadth of the corpus and that a summary article wouldn’t do it justice, but I personally wouldn’t see the harm in advancing the idea both via the book and via journals.
But it’s not suprising that Stubbs’ proposal hasn’t yet entered the mainstream. It took 56 years (1912 – 1968) before the idea of plate tectonics took hold. There was a long period where it was taboo to talk about it and controversial to conduct research on it. Uto-Aztecan would be at least as earth-shattering and paradigm-shifting for linguistics, archaeology, and anthropology as plate tectonics were for geology, and its religious implications will make the consensus even harder to break. If we get somewhere around 2070 without it doing so I might start to wonder, but with Stubbs’ evident tenacity and work ethic I wouldn’t be surprised if it something starts to break sooner than that.
Your quantitative approach to Uto-Aztecan was sorely needed. Before this post, I wasn’t quite sure what to make of the Uto-Aztecan topic. Now I can confidently say that cognates between Uto-Aztecan and Hebrew are strong evidence in favor of the authenticity of the Book of Mormon. However, the Uto-Aztecan evidence is still more difficult to digest than evidence associated with early modern English and chaismus, because expertise in Uto-Aztecan is so scarce.
Thanks Josh. I agree that this is the kind of evidence that can cause eyes to glaze over, and until such time as it becomes the mainstream consensus, all critics have to do is pretend it doesn’t exist (which is their primary tack for the EModE evidence). I hope I’ve done my bit, though, in terms of heading off the “correspondences can appear by chance” critique, which appeared to be favored line of the linguistically educated. It always seemed to me that 1500 would be a tough bar for chance to clear, and I’m encouraged that my analysis bears that out.
From Dr. Rasmussen’s reply to Robert F. Smith, the big takeaway I got from his reply is this, “it takes a lot of repetition to leave the realm of “coincidence” in the scientific world whenever it might be even distantly linked to religion.”
I know that isn’t quite what he said, but I’m convinced that if the Book of Mormon hadn’t entered into this discussion, it is my gut-feeling that Brian Stubbs’ work would have been hailed as a major breakthrough in linguistic familial relativity between Uto-Aztecan and the Semitic/Egyptian of the old-World. Because religion is even distantly correlated, then hesitancy for acceptance increases exponentially.
From all outward appearances, Brian Stubbs has gone to exceedingly great lengths to present his data, first, from a non-LDS view (or rather a purely academic view) and then later, with a shorter study directed at members. It will be interesting how this pans out over the next several years.
I know that this comment is naive, but I’m slightly confused why the distinct line between Mormon (sic) apologists and anti-Mormon detractors regarding this particular issue. (No, I’m not calling Chris Rogers an anti-Mormon.) What I don’t understand is why the incredibly strident attempts by those who aren’t linguists to define the actual relationship between Uto-Aztecan and Semitic languages as defined by Stubbs.
I mean, I’m not a linguist familiar with any of these languages, so I let the experts speak. I figure that if Brian Stubbs has done his research as well as he’s claimed, then his research will stand by itself. That attitude doesn’t seem to carry over to the other side, though, inasmuch as many of those with no more linguistic ability than the language they were born with opine on the issue as if they actually knew. This is what I believe is unconscionable, for these are the methods used to stifle research in the past.
Not only that, but even if Stubbs’ hypothesis is proven correct, that still doesn’t prove the Book of Mormon is true. It grants some potential basis for buttressing some claims as potentially demonstrated by Dr. Rasmussen, but I am uncertain what either side would gain by furthering the position. I mean, for all these detractors would then claim, Phoenicians and other mid-Eastern explorers with transoceanic voyages to the new-World could have left the requisite language prototypes, totally independent of the Book of Mormon.
Even though I find the study fascinating and helpful to me personally, I just don’t see how this one “wins” anyone over to either side.
Thanks for your thoughts, Tim.
In my view, if independent transoceanic voyages from Egyptians and Phoenicians are the only viable explanation for this evidence that the critical side can put forward, I don’t see how that would represent anything other than a significant concession. For one, it would reverse the typical position that transoceanic voyages are extremely unlikely if not impossible. This kind of language contact would probably imply that those voyages aren’t just possible, but that they were happening all the time.
Second, it would be tying the critics to a very strange string of coincidences, none of which would follow naturally from the idea of transoceanic voyages. If there was significant and frequent contact between the New and Old World, you’d expect it find evidence for it in the Carribean instead of on the Pacific coast. The Phoenicians in particular would have a hard time getting over there given that they were based in the Mediterranean. Not to mention that you’d have to explain how the Aramaic-laced Semitic came along for the ride.
The narrative provided by the BofM presents just about the only plausible way imaginable to get that peculiar mix of languages onto the Pacific coast of northern Mexico. If chance isn’t enough to get us Stubbs’ correspondences, critics may indeed try out some other options, but for me the only safe port in the Uto-Aztecan storm is authenticity.
Thank you for the response. This was excellent reasoning, formulated into a concise explanation. It was very much appreciated!
Vocabulary comparisons are only one aspect of Stubbs’ work. The other key element is the rules of linguistic transformation which Stubbs lays out in each instance. All his comparisons include systematically applied linguistic rules.
Non-LDS scholars have likewise found another set of strong correspondences within the language family of Oaxaca, Mexico, and I have summarized them online at https://drive.google.com/file/d/1C4GCVygshCm7eK7a_IAinsdEXko5cHOQ/view?usp=sharing .
Thanks Robert.
The consistent linguistic transformations are incorporated indirectly in my analysis by allowing for partial matches. In such cases, we’re accounting for the possibility that words could happen to match in a way that looked like consistent linguistic transformations, but were nevertheless flukes. Presumably chance could also produce many cases where the transformation didn’t look valid or consistent, but Stubbs would likely just ignore those cases whenever they popped up. My analysis suggests, though, that chance isn’t sufficient to give us the consistent transformations that Stubbs uncovered.
Your Oaxaca proposal is definitely intriguing. In terms of the ability for chance to produce those correspondences, though, it would depend how many words you (or other scholars) had to work through to produce them. If you had to comb through 1000 words to find a set of, say, 30 correspondences (I didn’t do a count of all the correspondences in your doc), then chance could definitely explain them. If it only took 100 words to get that many then chance is probably something we could rule out.
In the end, though, it’s probably going to take a number of analyses at the scale and detail of Stubbs’ effort, implicating a number of language families connected with BofM areas (and a robust demonstration that we can’t find those correspondences elsewhere) to have a shot at moving the secular consensus. I’m not going to hold my breath for that, but for the moment I’m satisfied that Stubbs work isn’t just a giant career-sized fluke.